Pollard's p − 1 algorithm

Pollard's p − 1 algorithm is a number theoretic integer factorization algorithm, invented by John Pollard in 1974. It is a special-purpose algorithm, meaning that it is only suitable for integers with specific types of factors; it is the simplest example of an algebraic-group factorisation algorithm.

The factors it finds are ones for which the number preceding the factor, p − 1, is powersmooth; the essential observation is that, by working in the multiplicative group modulo a composite number N, we are also working in the multiplicative groups modulo all of N's factors.

The existence of this algorithm leads to the concept of strong primes, being primes for which p − 1 has at least one large prime factor. Almost all sufficiently large primes are strong; if a prime used for cryptographic purposes turns out to be non-strong, it is much more likely to be through malice than through an accident of random number generation.

1 Base concepts
2 Multiple factors
3 Algorithm and running time
4 How to choose B?
5 Large prime variant
6 Implementations
7 References
8 See also
9 External links

Base concepts

Let n be a composite integer with prime factor p. By Fermat's little theorem, we know that for all integers a coprime to p and for all positive integers K:

$a^{K(p-1)} \equiv 1\pmod{p}$

If a number x is congruent to 1 modulo a factor of n, then the gcd (x − 1, n) will be divisible by that factor.

The idea is to make the exponent a large multiple of p − 1 by making it a number with very many prime factors; generally, we take the product of all prime powers less than some limit B. Start with a random x, and repeatedly replace it by $x^w \mod n$ as w runs through those prime powers. Check at each stage, or once at the end if you prefer, whether gcd (x − 1, n) is not equal to 1.

Multiple factors

It is possible that for all the prime factors p of n, p − 1 is divisible by small primes, at which point the Pollard p − 1 algorithm gives you n again.

Algorithm and running time

The basic algorithm can be written as follows:

Inputs: n: a composite integer

Output: a non-trivial factor of n or failure

select a smoothness bound B
$M \gets \prod_{\text{primes}~q \le B} q^{ \lfloor \log_q{B} \rfloor }$
randomly pick a coprime to n (note: we can actually fix a, random selection here is not imperative)
$g \gets \gcd(a^M - 1, n)$ (note: the powering can be done mod n)
if 1 < g < n then return g
if g = 1 then select a higher B and go to step 2 or return failure
if g = n then go to step 2 or return failure

If g = 1 in step 6, this indicates that for all p − 1 that none were B-powersmooth. If g = n in step 7, this usually indicates that all factors were B-powersmooth, but in rare cases it could indicate that a had a small order modulo n.

The running time of this algorithm is O(B × log B × log²n); larger values of B make it run more slowly, but are more likely to produce a factor.

How to choose B?

Since the algorithm is incremental, it can just keep running with the bound constantly increasing.

Assume that p − 1, where p is the smallest prime factor of n, can be modelled as a random number of size less than √n. By Dixon's theorem, the probability that the largest factor of such a number is less than (p − 1)^ε is roughly ε^−ε; so there is a probability of about 3⁻³ = 1/27 that a B value of n^1/6 will yield a factorisation.

In practice, the elliptic curve method is faster than the Pollard p − 1 method once the factors are at all large; running the p − 1 method up to B = 10⁶ will find a quarter of all twelve-digit factors and 1/27 of all eighteen-digit factors, before proceeding to another method.

Large prime variant

A variant of the basic algorithm is sometimes used; instead of requiring that p − 1 has all its factors less than B, we can require it to have all but one of its factors less than some B₁, and the remaining factor less than some B₂. Let p₁ be the smallest prime greater than B₁, p₂ the next-largest, and so on; let d_n = p_n − p_n−1. The distribution of prime numbers is such that the d_n will all be fairly small.

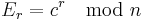Having computed $c = a^M \mod n$ , we can easily compute once and for all $E_r = c^r \mod n$ for all $r$ which appear as a value of $d_n$ . Compute $t_1 = c^{p_1} \mod n$ . We can then stop doing exponentiation, and compute

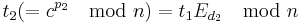$t_2 (= c^{p_2} \mod n) = t_1 E_{d_2} \mod n$ , $t_3 = t_2 E_{d_3} \mod n, \dots$

with one multiplication rather than one exponentiation at each step; this is quicker by roughly a factor log B than doing the exponentiations. It can also be accelerated significantly using Fast Fourier transforms.

Implementations

The GMP-ECM package includes an efficient implementation of the p − 1 method.
Prime95 and MPrime, the official clients of the Great Internet Mersenne Prime Search, use p - 1 to eliminate potential candidates.

References

Pollard, J. M. (1974), "Theorems of Factorization and Primality Testing", Proceedings of the Cambridge Philosophical Society 76 (3): 521–528, doi:10.1017/S0305004100049252

External links

Pollard's p − 1 Method

Number-theoretic algorithms

Primality tests	AKS · APR · Baillie–PSW · ECPP · Elliptic curve · Pocklington · Fermat · Lucas · Lucas–Lehmer · Lucas–Lehmer–Riesel · Proth's theorem · Pépin's · Solovay–Strassen · Miller–Rabin · Trial division

Sieving algorithms	Sieve of Atkin · Sieve of Eratosthenes · Sieve of Sundaram · Wheel factorization

Integer factorization algorithms	CFRAC · Dixon's · ECM · Euler's · Pollard's rho · p − 1 · p + 1 · QS · GNFS · SNFS · rational sieve · Fermat's · Shanks' square forms · Trial division · Shor's

Multiplication algorithms	Ancient Egyptian multiplication · Karatsuba algorithm · Toom–Cook multiplication · Schönhage–Strassen algorithm · Fürer's algorithm

Discrete logarithm algorithms	Baby-step giant-step · Pollard rho · Pollard kangaroo · Pohlig–Hellman · Index calculus · Function field sieve

GCD algorithms	Binary GCD · Euclidean · Extended Euclidean · Lehmer's

Modular square root algorithms	Cipolla · Pocklington's · Tonelli–Shanks

Other algorithms	Chakravala · Cornacchia · integer relation algorithm · integer square root · Modular exponentiation · Schoof's

Italics indicate that algorithm is for numbers of special forms; bold indicates deterministic algorithm for primality tests (current article is always in bold).